Borges y yo (y tú también)
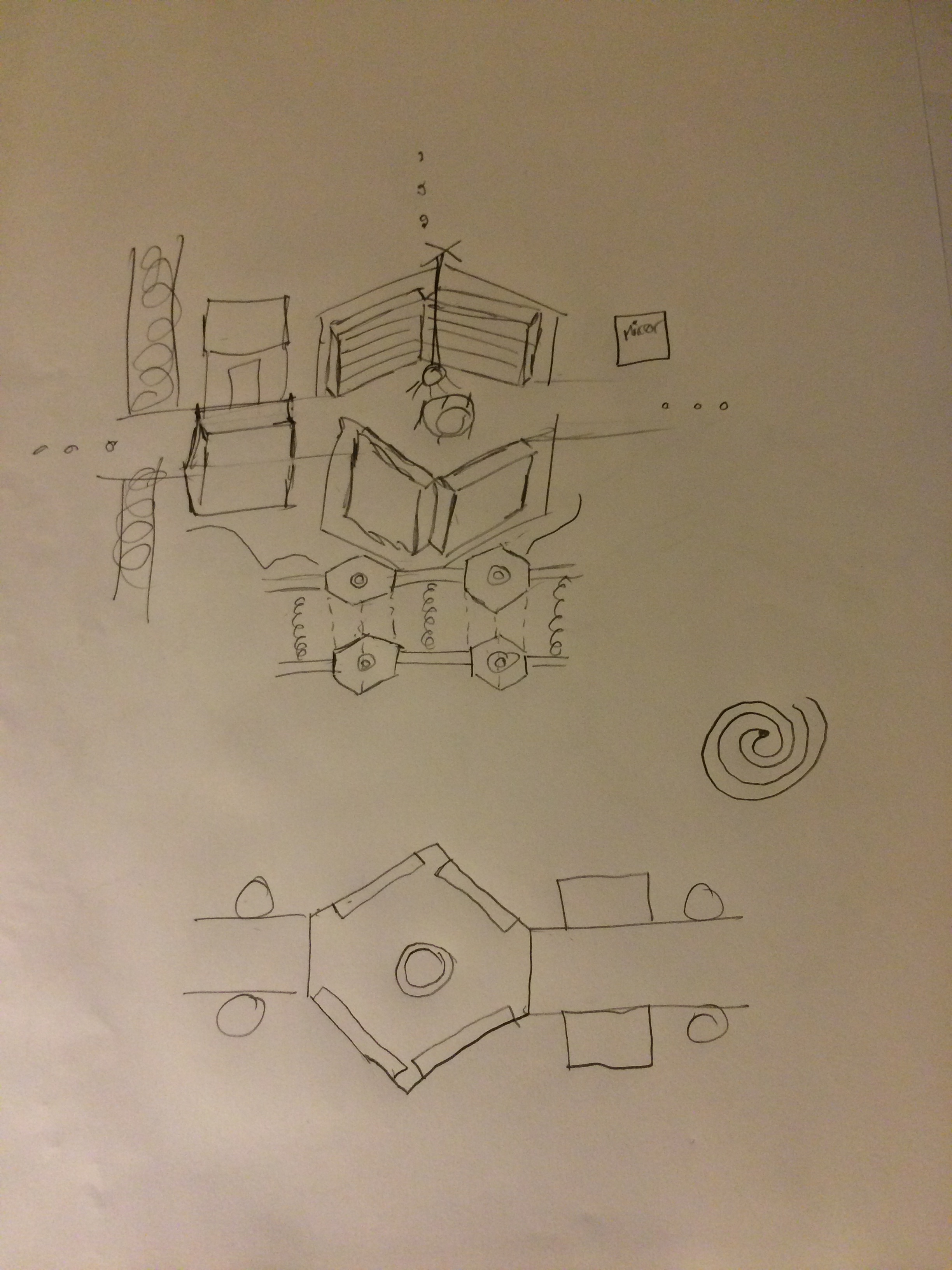
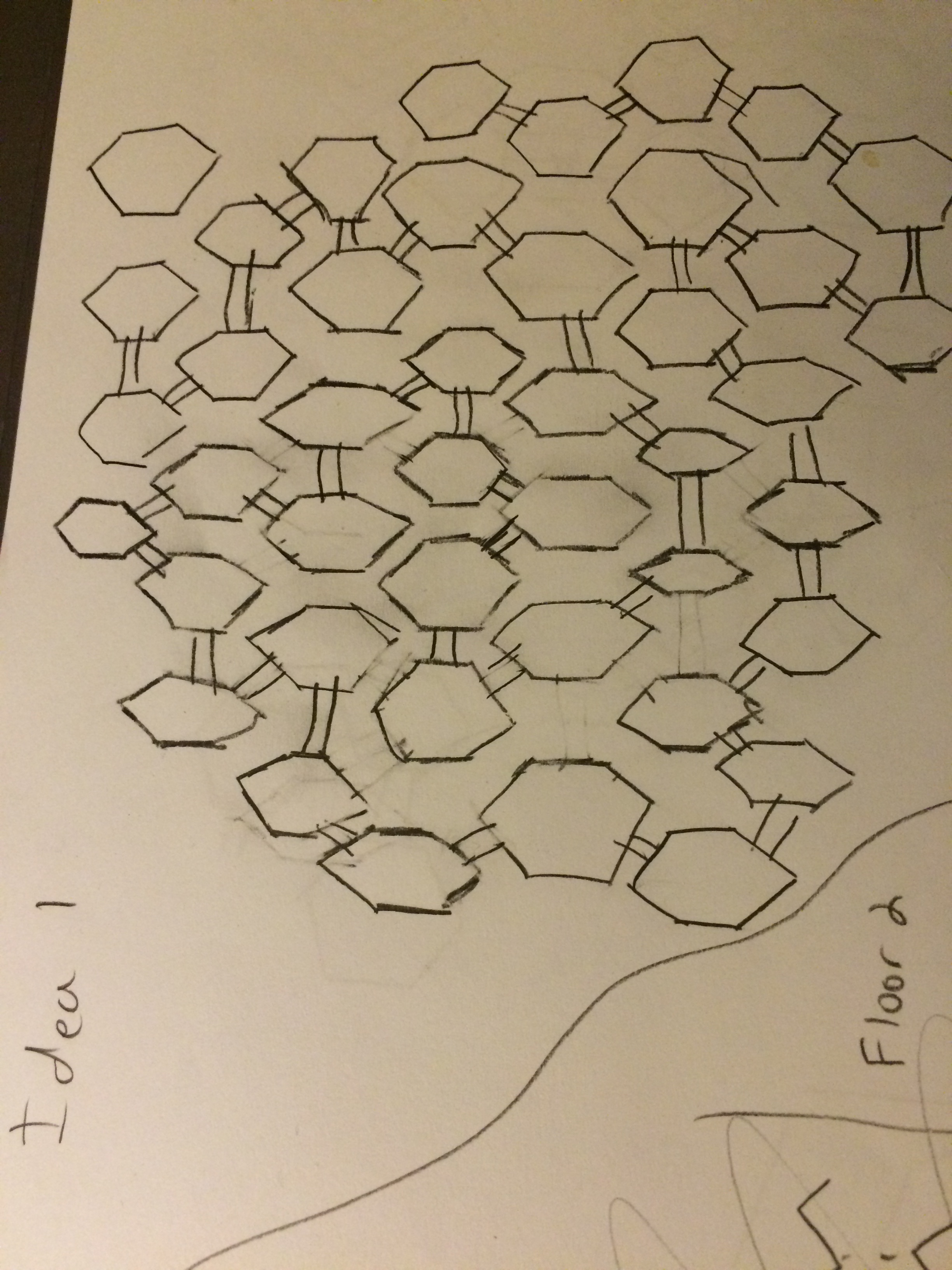
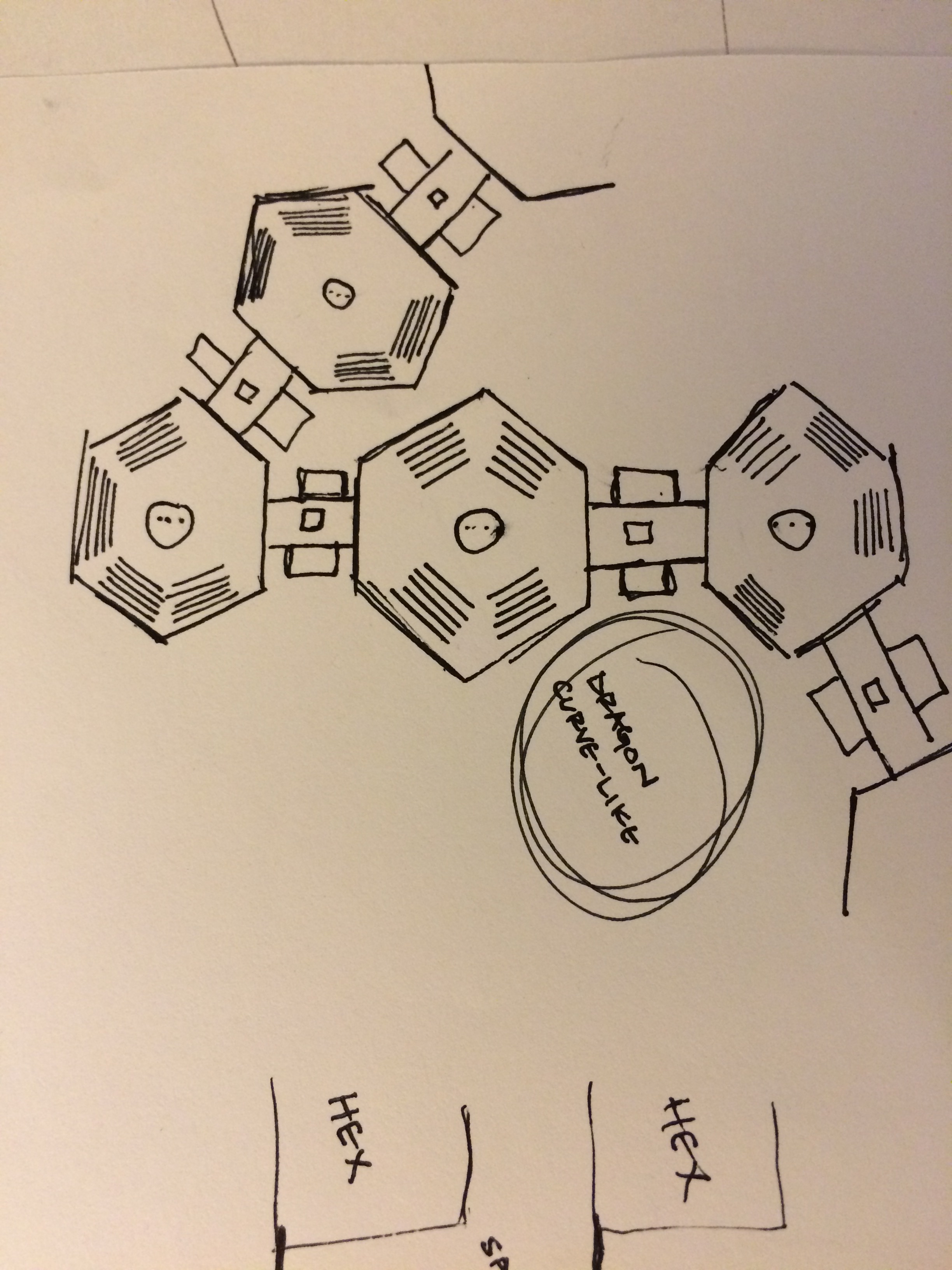
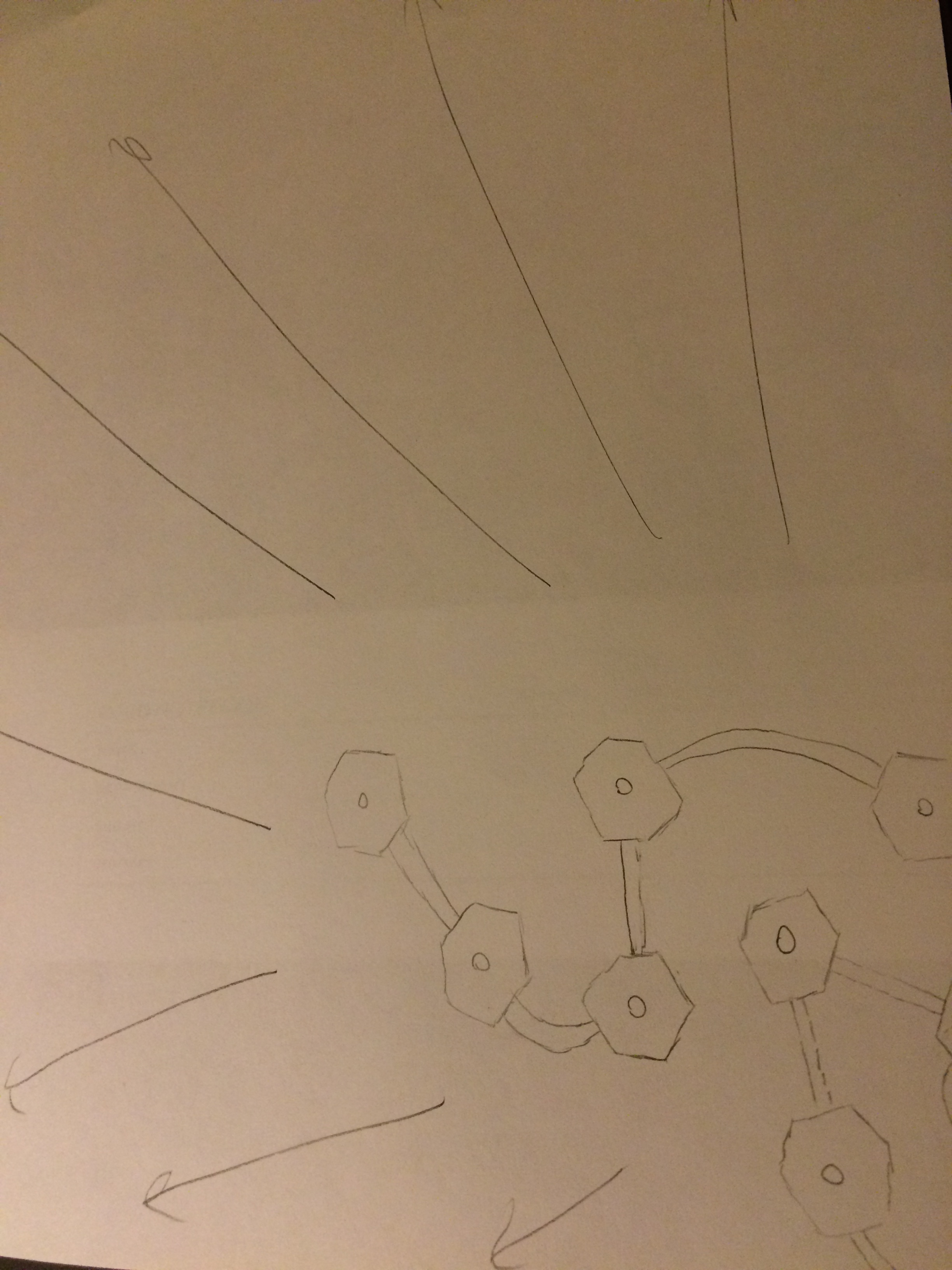
/Jorge Luis Borges, perhaps more than any other writer of his stature, weaves mathematics into the structure of his stories so completely that it can take an immense amount of analysis to unravel them. I'm not entirely sure that Borges thought this was worthwhile; indeed, during interviews he often took gentle jabs at literary analysts who spent so much time and hand-wringing over his work. But it's so difficult to resist. I mean, I dare you to read The Library of Babel and not get sucked into trying to figure out the structure of the thing. At the beginning of class last week, I asked the students to spend a few minutes sketching what they thought the Library looked like. Here are a few of their renditions (click on them to scroll).
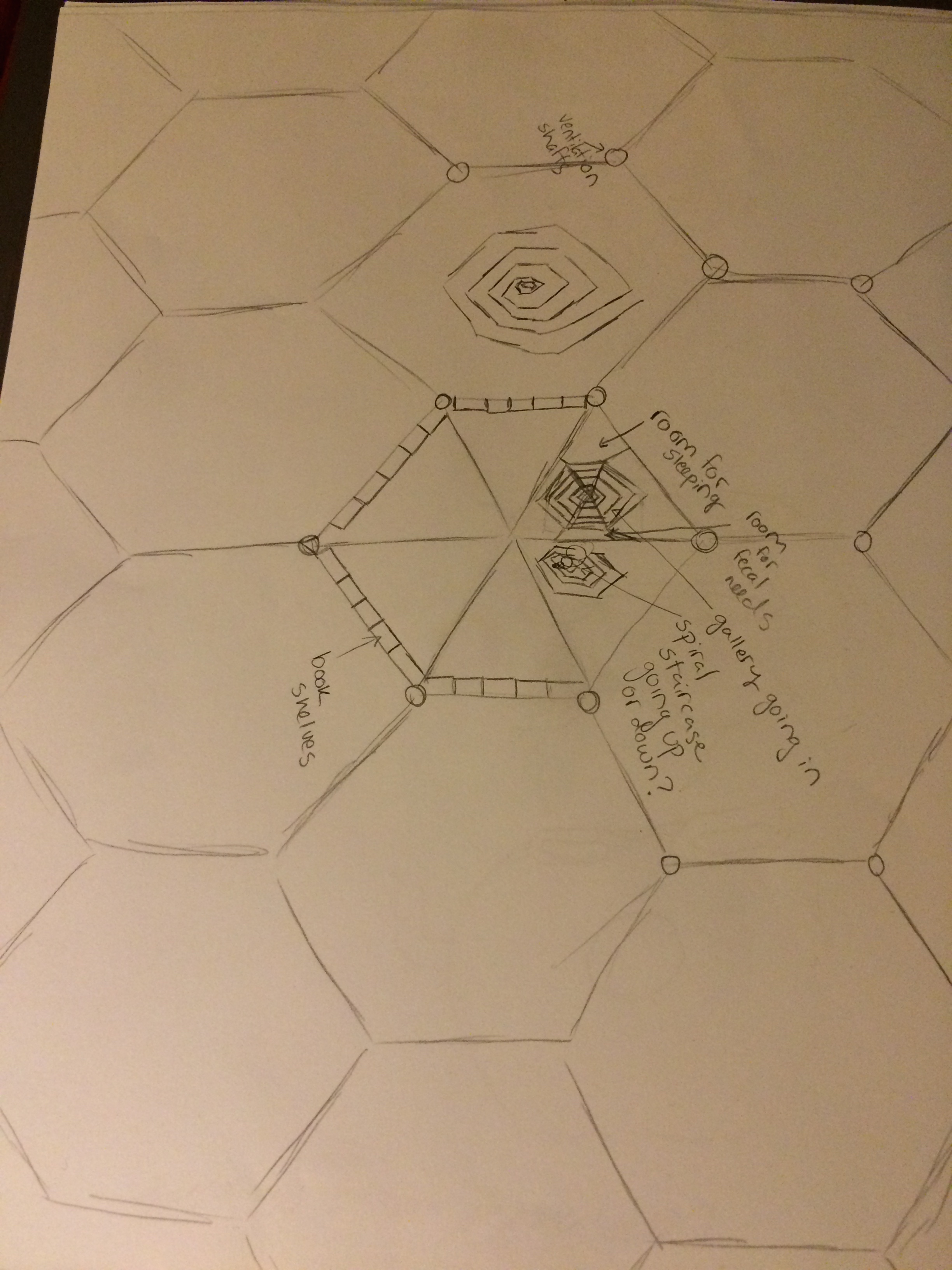
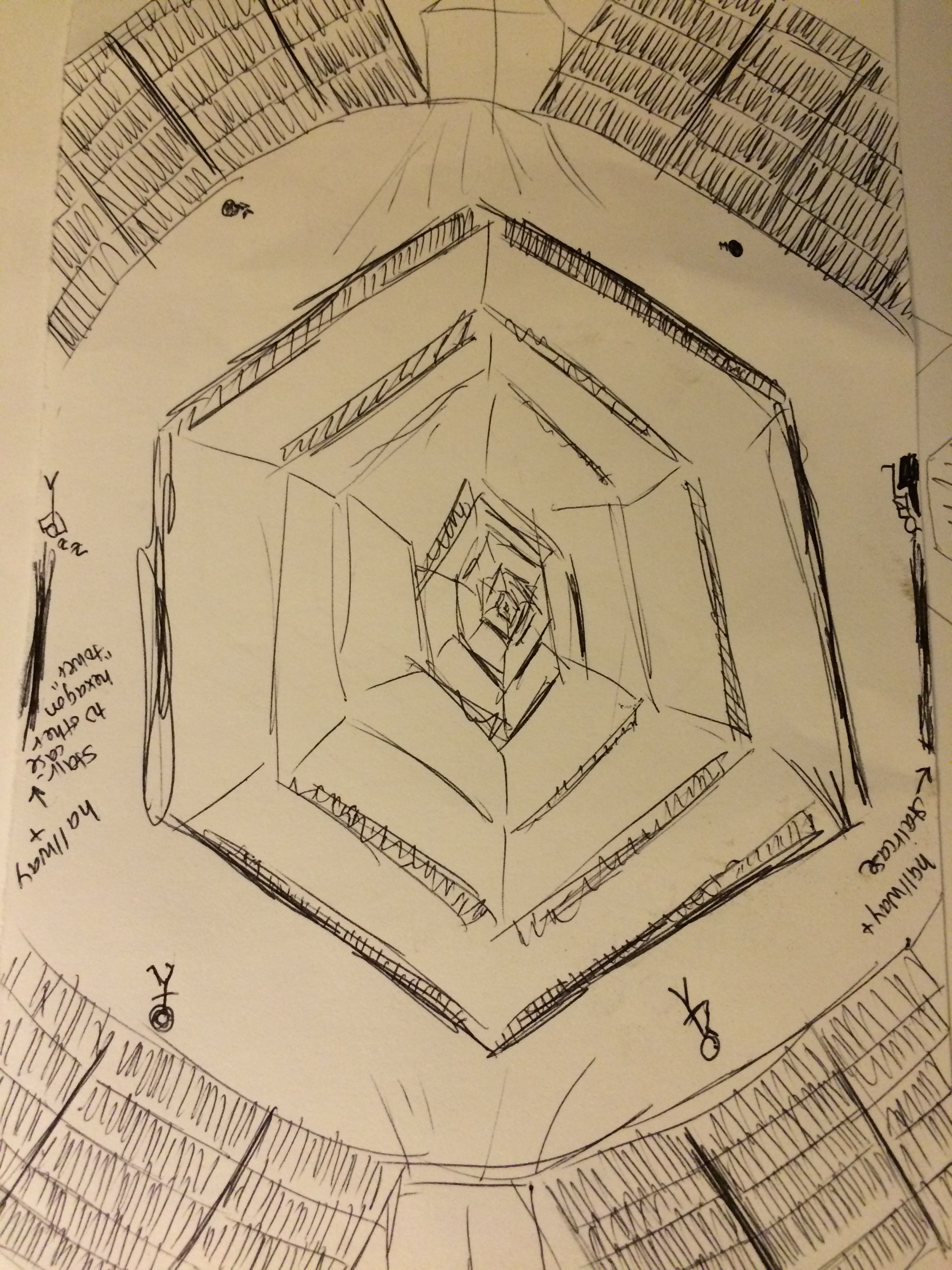
You see lots of hexagons because Borges spends some time telling us the structure of the rooms in the Library: each gallery is hexagonal, bookshelves line four walls, there are two free walls. The following passage in the story says a lot, but leaves open plenty of room for interpretation: One of the hexagon's free sides opens onto a narrow sort of vestibule, which in turn opens onto another gallery, identical to the first--identical in fact to all. To the left and the right of the vestibule are two tiny compartments. One is for sleeping, upright; the other is for satisfying one's fecal necessities. Through this space, too, there passes a spiral staircase, which winds upward and downward into the remotest distance.
At first read, then, I immediately conclude that each of the two free sides opens to another hexagon. Even this was disputed by some students. Maybe there's nothing on the other free side, or maybe there's a bench for sitting to read, and all the hexagons wrap around the staircase, forming a sort of Tower of Babel shaped library. Maybe. If this is indeed the case, then each floor of the library would contain only finitely many cells, and I don't really think this is what Borges had in mind (or maybe he did--you never know). The sentence in Spanish isn't any clearer: Una de las caras libres da a un angosto zaguán, que desemboca en otra galería, idéntica a la primera y a todas.
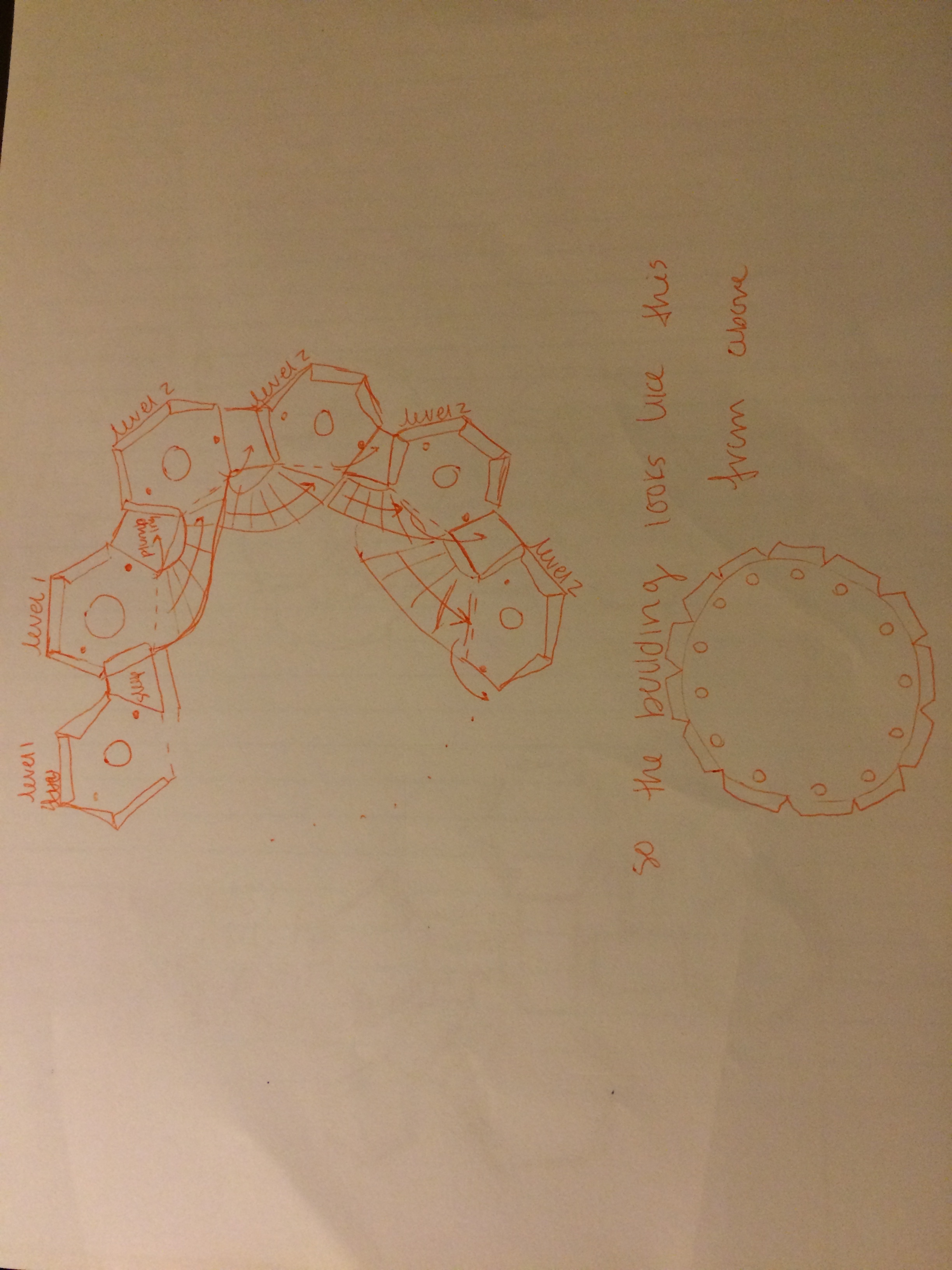
Even if you accept the premise that each of the free sides leads to another gallery, there's still a lot of ambiguity. Just how "identical" are these cells? If we mean the free sides are always opposite each other, then we get a particular structure: the cells line up, extending infinitely along a line in each floor and then these rows stack on each other vertically. Maybe. But what if there is a staircase in only one of the corridors joining two cells? Note that Borges isn't clear on this point--una de las caras libres... He doesn't say solamente una, which would mean exactly one staircase. If there is a staircase in each passage, then the geometry of the Library is fixed--each floor must look like all the other floors. But if there is only one staircase for each pair of cells, then more interesting things can happen--we could have a different layout for each floor.
Also, if we don't insist that the free sides are always in the same positions in each cell, then we can get all sorts of labyrinthine structures on each floor. And, these labyrinths can be so elaborate that two cells that share a wall can be arbitrarily far apart in the sense that a librarian would have to walk through a huge number of galleries to get from one to the other (here, "huge" means that for any positive integer \( n\), there are adjacent galleries which require a librarian to pass through at least \( n\) cells to get from one to the other). This can be ok if we are in the one staircase to a pair model because we may then be able to go up or down a few floors to make our way to an adjacent cell, thereby skipping the labyrinth on a particular floor.
Wait a minute. We haven't even begun to discuss what this story is about. We are arguing about the structure of the damn Library. I later read this on Twitter from one of the students in the class:
“when you spend over an hour talking about hexagons in a class and it turns into a heated discussion...”
Yeah, we did just that. Hexagons \(\Longrightarrow\) intense discussion. Could a mathematician ask for more?
We'll get around to the meaning of this story in class this week. For now, let's think about how many books are in the Library. Borges tells us that each book has \(410\) pages, each of which has \(40\) lines of \(80\) characters. He also tells us that the alphabet consists of \(22\) characters along with a space, period, and comma. That makes \(25\) orthographic characters. We are told the Library is complete; that is, every possible book is in it. This is a finite number. In fact, each book consists of \(410\times 40\times 80 = 1,312,000\) characters, and since each of these may be any of the \(25\) possibilities, there are \[N=25^{1,312,000} \approx 10^{1,834,097}\] distinct books. This is an enormous number (although, next to infinity it is effectively zero). To give you some perspective on how large \(N\) is, if the known universe were filled with nothing but protons (and nothing else, no blank space) it would only contain about \(10^{126}\) of them. So the Library can't exist in our universe; there just isn't room.
There are all sorts of odd books in the Library. There is a completely blank book. There is a book that is blank except that it has a period in the middle of page 193. There is a book with nothing but the letter x. There are \(1,312,000\) books that have a single letter x. The tweet quoted above appears exactly as it is in \(25^{1,311,898}\) of the books in the Library. This blog post appears in a huge number of the books (if we write out the numbers and ignore the improper punctuation), in every language spoken on Earth (if transcribed into the alphabet), and in any language spoken on any other planet (do you really think we're alone in the universe?).
Question: how would you find a particular book in the Library? Is there any hope? Maybe it's enough to know it's there, just like mathematicians are often satisfied with existence proofs. In any case, it's not hard to see that a given librarian may not be able to reach a particular book in his lifetime, even if he knows where it is. Is this cause for despair?
I'll save the philosophy for next time. For now, one final remark. William Goldbloom Bloch has written a wonderful book, The Unimaginable Mathematics of Borges' Library of Babel, that talks about a lot of this mathematics in far greater detail. I suggest picking it up if you are so inclined. Or you can walk the Library for yourself, seeking out its meaning.